系统辨识 & 自己蠢蠢的想法

发表于 | 阅读次数:

系统辨识——通过预测减少信息延时的方法：

我个人理解的系统辨识是通过系统历史输入输出数据得出一个数学模型模拟该实际系统，如果辨识出的模型和真实模型拟合程度高的话，那么对之后的任何一组新数据，我们都可以知道它输入到该系统之后系统的输出，换个更加口语化的表述：我们可以在系统作出对一个输入的响应之前预测该响应，举一个简单的例子，空调-房间模型：房间室温为30摄氏度，此时空调以 10KW 的功率制冷，那么一分钟后室内温度会变成多少度？或者说室内温度变化曲线是怎么样的？在平时，在一个特定时刻之前我们无法获得这个时刻之后的温度曲线，例如在2点时我们无法获得2点以后的温度曲线，当且仅当时间轴运行到该时刻我才能获得该时刻的输出信息，而且很多情况下，是该时刻之前的历史信息。从另一种角度来说，我们被动地被系统的时间特性牵绊住，最多做到获取信息无滞后，而无法超前获得信息。而系统辨识就是提供了一种超前获取系统输出信息的方法，他利用真实的系统输入输出数据去构建一个数学模型，当这个模型足够有效时，我们就可以利用这个模型计算之后的输入对应的系统输出，从而为我们在争取了时间上的优势。

实例分析

在本例子中，系统有7个输入，4个输出，一共有4000组数据

7输入4输出，首先根据输出进行划分，7个输入分别对于4个输出都有影响，也就是说存在着4*7=28个影响通道，我们将整个系统分成四个子系统，利用7个数据分别构建四个多输入单输出子模型：

1
2
3
4
5
6
7
8
假设 
    四个输出 为 Out1 Out2 Out3 Out4
    七个输入 为 InPut1 InPut2 InPut3 InPut4 InPut5 InPut6 InPut7
那么 
    Out1 = model1( InPut1 InPut2 InPut3 InPut4 InPut5 InPut6 InPut7 ) 
    Out2 = model2( InPut1 InPut2 InPut3 InPut4 InPut5 InPut6 InPut7 ) 
    Out3 = model3( InPut1 InPut2 InPut3 InPut4 InPut5 InPut6 InPut7 )  
    Out4 = model4( InPut1 InPut2 InPut3 InPut4 InPut5 InPut6 InPut7 )

对于每个Model的辨识 ，我们都需要知道如何各个Input对于Out的影响通道，每一个Input对于Out都有他的影响方式，因此上述的表达式可以转化为：

1
2
Out k = model k1(input1) + model k2(input2)+model k3(input3)+model k4(input4)+model k5(input5)+model k6(input6)+model k7(input7)
k = range(1:4)

其中model kj 代表 Input j 对于 Out k的影响通道，其实我们要辨识的是28个SISO模型。那么如何去辨识一个SISO模型呢？我们还需要知道 Input j 对于 Out k的影响延时（也就是一个输入要过多久才能影响到Out k当中去）以及 Input j 对于 Out k 的影响阶数（因为系统的Out k是一个对于历史输入的综合响应,换句话说，t时刻的Out可能是由 t-k ～ t时刻的输入共同影响的结果，而k就是阶数）

1
Out(t) = A0*Input(t) + A1*Input(t-1) + A2*Input(t-2) ……

因此我们对于每个SISO模型都需要确认这两个参数，在这里我们采用一种很笨重的方法（至少在我看来）我们遍历一些可能的Delay和Order分别辨识模型（这里不是简单的遍历两个参数，有种迭代的算法不详细展开），然后选取一个拟合优度最小的参数组合，去辨识参数

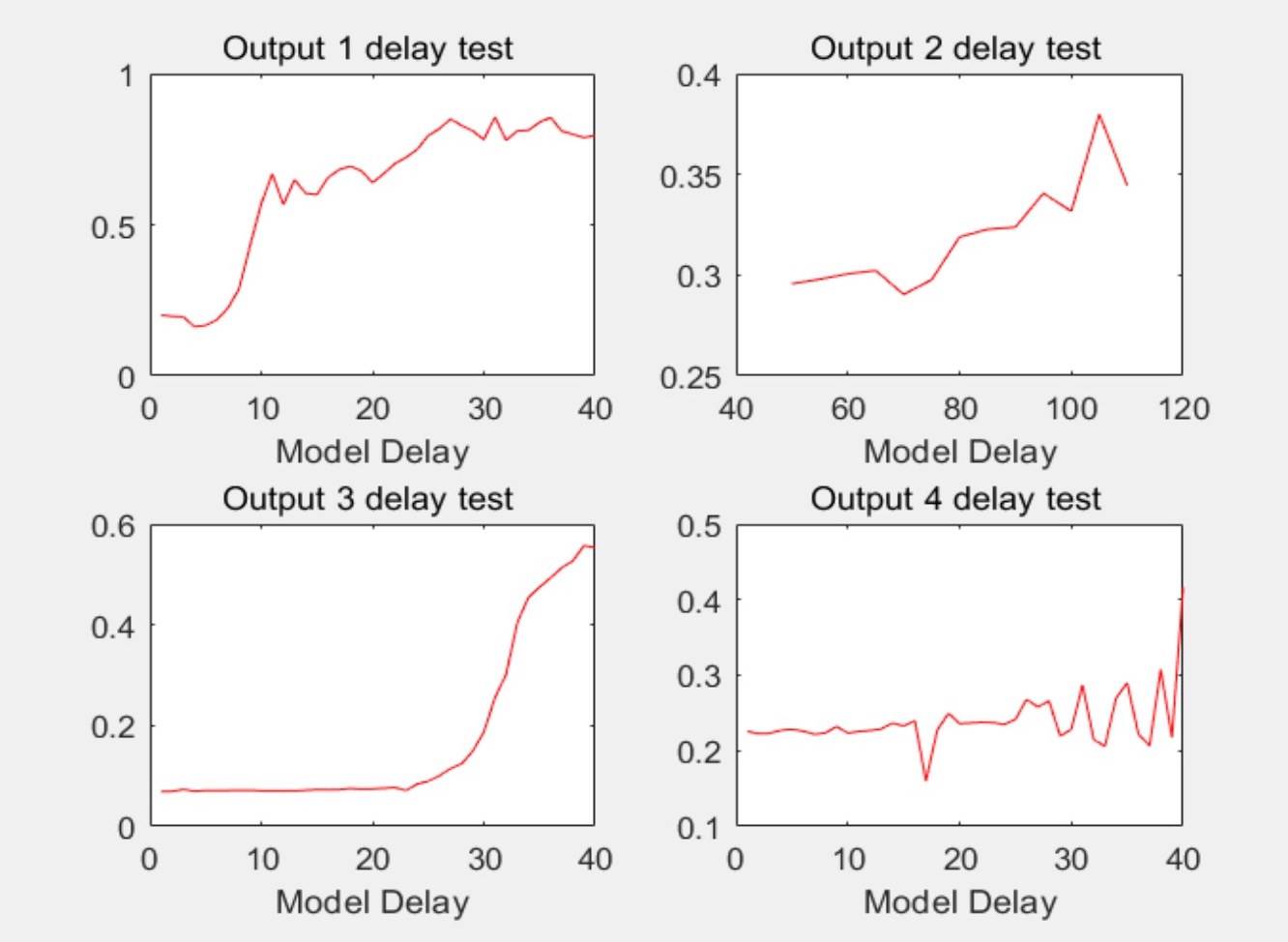
Delay选择

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
load crudedata
test = 1:40 ;
for Delay = test
    Arx1Model = armax( [CVDATA(:,1) MVDATA] , [10 10 10 10 10 10 10 10 10 Delay Delay Delay Delay Delay Delay Delay],30) ;
    Error1 = CVDATA(:,1) - idsim(MVDATA,Arx1Model);
    Vest(Delay) = cov(Error1); 

    Arx1Model3 = armax( [CVDATA(:,3) MVDATA] , [10 10 10 10 10 10 10 10 10 Delay Delay Delay Delay Delay Delay Delay],30) ;
    Error3 = CVDATA(:,3) - idsim(MVDATA,Arx1Model3);
    Vest3(Delay) = cov(Error3);

    Arx1Model4 = armax( [CVDATA(:,4) MVDATA] , [10 10 10 10 10 10 10 10 10 Delay Delay Delay Delay Delay Delay Delay],30) ;
    Error4 = CVDATA(:,4) - idsim(MVDATA,Arx1Model4);
    Vest4(Delay) = cov(Error4);
end
test2 = 50:5:110 
for Delay2 = 50:5:110
    Arx1Model2 = armax( [CVDATA(:,2) MVDATA] , [10 10 10 10 10 10 10 10 10 Delay2 Delay2 Delay2 Delay2 Delay2 Delay2 Delay2],30) ;
    Error2 = CVDATA(:,2) - idsim(MVDATA,Arx1Model2);
    Vest2(Delay2) = cov(Error2);
end 

figure
subplot(221),plot(1:40,Vest ,'-r' );
title('Output 1 delay test ');
xlabel('Model Delay');

subplot(222),plot(test2,Vest2(50:5:110) ,'-r' );
title('Output 2 delay test ');
xlabel('Model Delay');

subplot(223),plot(1:40,Vest3 ,'-r' );
title('Output 3 delay test ');
xlabel('Model Delay');

subplot(224),plot(1:40,Vest4 ,'-r' );
title('Output 4 delay test ');
xlabel('Model Delay');

Order选择

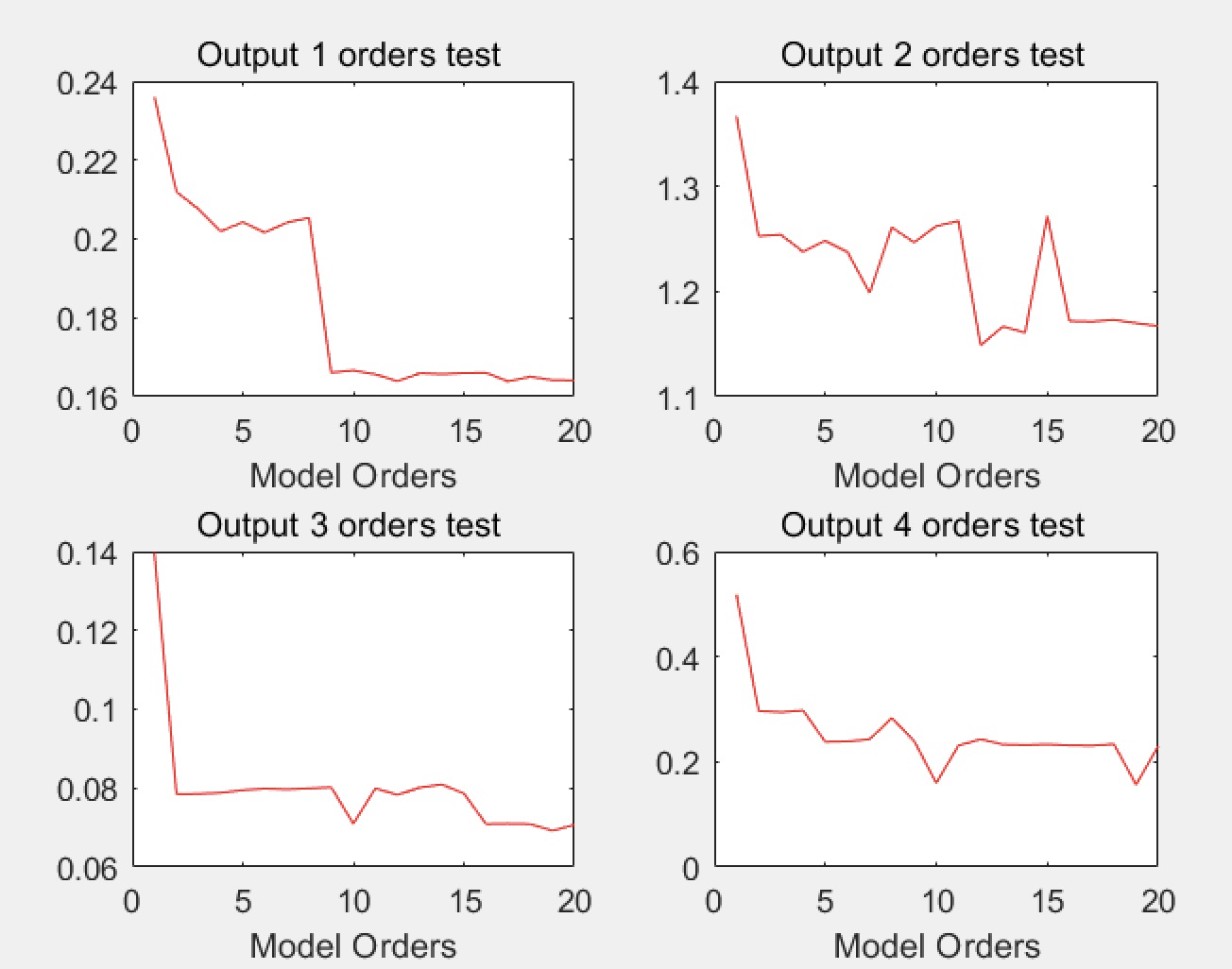
result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
load crudedata
Delay1 = 5 ;
Delay2 = 70 ;
Delay3 = 23 ;
Delay4 = 17 ;
iter =30 ; 

% Use armax model to select_order
ords = 1:20 ;
for n = ords
    ArmaxModel = armax( [CVDATA(:,1) MVDATA] , [n n n n n n n n n Delay1 Delay1 Delay1 Delay1 Delay1 Delay1 Delay1],30) ;
    Error1 = CVDATA(:,1) - idsim(MVDATA,ArmaxModel);
    Vest(n) = cov(Error1); 
    
    ArmaxModel2 = armax( [CVDATA(:,1) MVDATA] , [n n n n n n n n n Delay2 Delay2 Delay2 Delay2 Delay2 Delay2 Delay2],30) ;
    Error2 = CVDATA(:,2) - idsim(MVDATA,ArmaxModel2);
    Vest2(n) = cov(Error2); 
    
    ArmaxModel3 = armax( [CVDATA(:,3) MVDATA] , [n n n n n n n n n Delay3 Delay3 Delay3 Delay3 Delay3 Delay3 Delay3],30) ;
    Error3 = CVDATA(:,3) - idsim(MVDATA,ArmaxModel3);
    Vest3(n) = cov(Error3); 

    ArmaxModel4 = armax( [CVDATA(:,4) MVDATA] , [n n n n n n n n n Delay4 Delay4 Delay4 Delay4 Delay4 Delay4 Delay4],30) ;
    Error4 = CVDATA(:,4) - idsim(MVDATA,ArmaxModel4);
    Vest4(n) = cov(Error4); 
end

figure
subplot(221),plot(1:20,Vest ,'-r' );
title('Output 1 orders test ');
xlabel('Model Orders');

subplot(222),plot(1:20,Vest2,'-r' );
title('Output 2 orders test ');
xlabel('Model Orders');

subplot(223),plot(1:20,Vest3 ,'-r' );
title('Output 3 orders test ');
xlabel('Model Orders');

subplot(224),plot(1:20,Vest4 ,'-r' );
title('Output 4 orders test ');
xlabel('Model Orders');

对上两个步骤进行迭代直到得到一个好的拟合优度

残差分析

1
…………

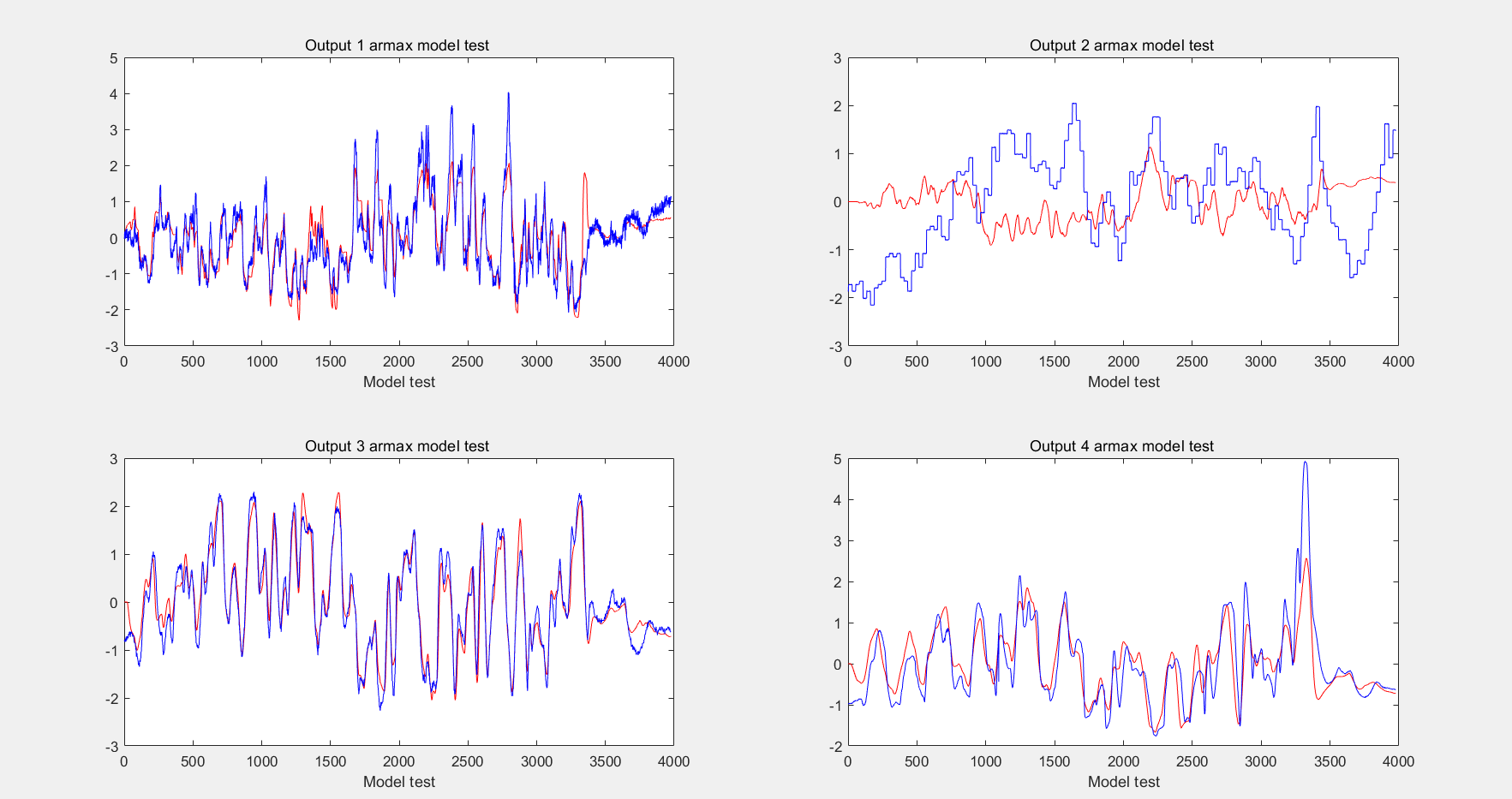
模型检验

result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
load crudedata
Delay1 = 5 ;
Delay2 = 70 ;
Delay3 = 23 ;
Delay4 = 17 ;
iter =30 ; 

% Use armax model to select_order

ArmaxModel = armax( [CVDATA(:,1) MVDATA] , [3 3 3 3 3 3 3 3 3 Delay1 Delay1 Delay1 Delay1 Delay1 Delay1 Delay1],30) ;
out1 = idsim(MVDATA,ArmaxModel);

    
ArmaxModel2 = armax( [CVDATA(:,1) MVDATA] , [7 7 7 7 7 7 7 7 7 Delay2 Delay2 Delay2 Delay2 Delay2 Delay2 Delay2],30) ;
out2 = idsim(MVDATA,ArmaxModel2);

    
ArmaxModel3 = armax( [CVDATA(:,3) MVDATA] , [2 2 2 2 2 2 2 2 2 Delay3 Delay3 Delay3 Delay3 Delay3 Delay3 Delay3],30) ;
out3 = idsim(MVDATA,ArmaxModel3);


ArmaxModel4 = armax( [CVDATA(:,4) MVDATA] , [2 2 2 2 2 2 2 2 2 Delay4 Delay4 Delay4 Delay4 Delay4 Delay4 Delay4],30) ;
out4 = idsim(MVDATA,ArmaxModel4);
 


figure
subplot(221),plot(1:3977,out1 ,'-r' , 1:3977 , CVDATA(:,1) ,'-b'  );
title('Output 1 armax model test ');
xlabel('Model test');

subplot(222),plot(1:3977,out2,'-r' , 1:3977 , CVDATA(:,2) , '-b' );
title('Output 2 armax model test ');
xlabel('Model test');

subplot(223),plot(1:3977,out3 ,'-r' , 1:3977 , CVDATA(:,3) ,'-b' );
title('Output 3 armax model test ');
xlabel('Model test');

subplot(224),plot(1:3977,out4 ,'-r' , 1:3977 , CVDATA(:,4) , '-b' );
title('Output 4 armax model test ');
xlabel('Model test');

系统辨识的用处

例子当中的系统其实是一个工业系统，他的7个input基本上能说是整个系统的有效input了，但是如果系统辨识要用到金融系统当中去，我不否认金融系统可以抽象成一个动态模型，并且金融系统和过程工业系统可以说有很多地方可以比拟，打个比方动态性上，金融系统也是一个不折不扣的动态系统，并且他也存在着时延，可能在过程工业系统中，利用系统辨识忽略系统的时延去预测系统的输出能够给设计控制算法带来优势，进而提高过程工业的动态特性，但如果是金融系统，假设系统辨识忽略了金融系统的时延去预测系统的输出带来的可是超前的信息，在最早以前，花费巨额资金铺设光缆只为减少证券交易市场信息0.001s的时延，如果现在能够超前于系统响应得到预测响应，无疑是一种点金术。

我存在的疑问

前言提到我不否认金融可以抽象成一个系统，那么要对他进行辨识，不谈别的，就需要明确输入输出是什么？以及如何获得输入输出数据。首先金融系统不是随随便便能够加载测试数据的，假设不计成本你加载了测试数据获得测试输出，但是整个金融系统其他端的输入，世界上各个资本对于系统的输入只能当作噪声，如果你加载的信号微乎其微，那么可能输入输出之间的关系可能就没什么意义，因为信噪比太小了。

那么系统就真的不可辨识吗？

持保留意见，大二修习的另一门课程让我思考这个问题时有另一种维度，在以上的讨论中我们把金融系统抽象成了一个系统，或者说压根不是抽象，因为的的确确金融系统存在并且拥有很多和过程工业系统类似的特性。甚至对于过程工业系统来说，可以通过机理建模的方式得到系统的真实模型，那需要扎实的理论功底。对于金融系统，或许利用数学建模也能构建一个模型描述它，毕竟他是一个构建在一些金融规则之上兆输入多输出的模型，而输出和输入的模型基于金融规则，并且时延 >= 0,这点毋庸置疑，我们要预测系统未来的输出有两个难点：

1
2
1)我们无法获得兆级的输入信息：金融系统的输入太多了，个体的输入太过微乎其微，因此系统输出-个体输入之间的模型是难以辨识的.
2)输出和下一时刻输入之间的耦合关系还包含着兆级个体的博弈策略，这点怎么解释呢？就是说t时刻的输出对于t+1时刻各个用户的输入肯定是有关联的，因为每个金融系统中的参与个体都有自己对于金融系统的理解，并且对于金融系统的输出有自己的考量，他们会用自己的投资策略去决定下一时刻的输入.

因此停留在和众金融系统参与者一样的角度去构建金融系统，尝试想要辨识他是困难和无效的：
首先成本高，为了提高信噪比，你要保证测试数据对于系统有一个好的影响程度
再谈假设不计成本，没有辨识的意义：
. 首先：我觉得金融系统的系统模型被规则明确，去辨识这个系统没有意义，我可以用金融规则去描述系统
. 其次：因为你加入了足以影响系统的测试数据，会影响到其他参与者的策略，因此这样辨识出的模型在之后新数据时可能没有很好的拟合度

换一种角度去抽象系统

我们能否站在更高的角度去抽象系统呢？我们把金融规则+兆级参与者都囊括为一个系统中的内参，而此时的系统输入便为前一秒系统的输出：金融系统的参与者很多，他们拥有不同的对于系统的影响能力，他们也有不同的参与策略，但现在这些都成为一个系统的内参，换句话说：整个系统输入可能是当前时刻之前的系统输出，因为参与者组成的一个抽象人群他们对于系统的输出有自己的理解，假设活跃在同一金融市场的主流参与者在一定时期内活动特性是继成习惯的，那么现在的系统辨识就是去辨识一定时间段内该金融系统的参与者人群对于系统历史输出的响应策略， 这个系统应该是实时的，因为他表征了一个金融系统参与人群的博弈策略，我们做出了参与人群在一定时间内不会大变动的假设：即一个金融系统中的参与人群在一定时间内有着类似的投资策略，现在的系统辨识就是要去辨识这个投资策略，他有时效性，但只要这样的系统能够在一个周期内有着不错的拟合度，那我丝毫不吝啬让我的私人服务器去辨识这个模型，只要他能够在一个模型有效期间内给出答案，就是有意义的。

总结

记得“惊天魔盗团”里面有那么一句话，只有脱离于社会才能真正影响社会，我们如果站在金融系统内部去加测试信号，那要真正掌控这个金融系统很难。那么站在更高一维度呢？也许真的是可行的，最近呆呆搞了一个基金量化交易的模型，一直以来的兴趣被激发了，试试呗，反正想法不花钱。