浅谈求解函数的“全局”最小值

发表于 | 阅读次数:

x = tanx在[0,π／2]上解是多少

在很多时候,利用常规高等数学求解一个函数是行不通的,随便举个例子,求解 x = tanx 在[0,π／2]的解,你能利用常规高等数学解出x吗？如果真的想解,超越方程了解一下.但今天我在这里要介绍的是两种其他的解法,一种是在和BC讨论之后完善的想法,另一种是小黑告诉我的,其实我在系统辨识这门课程当中也有接触过,但是仅停留在知道有这个名词,不具体理解的阶段.

从一道简单的数学题说起

先来简单看看下面这题:

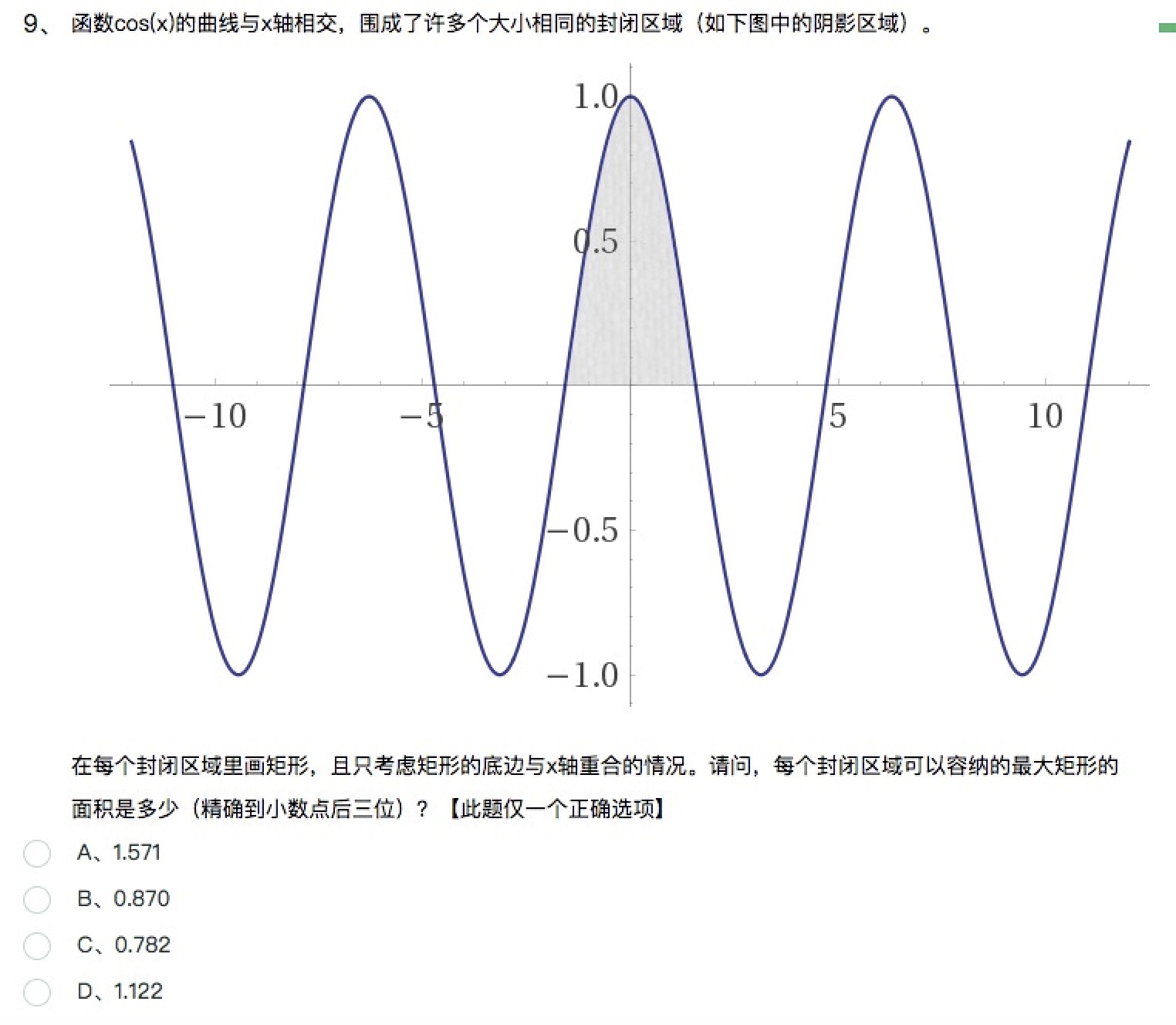
result

碰到这题的时候，我正在做饭(说的具体点,是刚吃完自己做的饭),当时下意识地去设了一个x
然后列出面积的表达书 S = F(x),想通过常规数学运算应该可以直接求解出最大值。我设一个矩形宽为
2x,那么易得矩形高为 cosx, 那么 S = F(x) = 2xcosx,直接求导 0.5*F(x) = cosx - xsinx 在[0,π／2]上,F(x)递减,且F(0) >0 F(π／2)<0 也就意味着原函数先递增后递减,最大值在导数为
0处取,也就是说现在的问题变成了:

1
2
F`(t) = cost - tsint = 0
tcost = ？

走到这步很简单,但之后让我懵逼了,F`(t) = cost - tsint = 0 如何解？

冷静思考之后我有了初步的答案

首先我明确这依靠我所掌握的浅薄的数学知识是无法求解出这个答案的,那么我对于这个问题能做什么呢？我是否可以利用试根的办法去试出解呢？

试根？真的要这么蠢吗？

对!试根是可以的,就像开方运算一样,因为函数的单调性我已经掌握了,他的导数是单调递减的,我可以用试根的方法求解出一个近似值,只要我有耐心,找到一个近似值应该不是难事,但这太蠢了.我是不是能够找到一种试根的方法,让每一次试根都有效率一点,而不是盲目地瞎试呢？并且这个试根的方法要能保证我最终能够找到或者说逼近真实的解.那我如何去构造这个试根的算法呢？

解法一: 牛顿迭代带来的灵感

之前就了解过牛顿迭代开方的操作,一直印象深刻,那么这样的迭代方法是否能够运用在这里呢？让我来看看目标函数 cost - tsint = 0 ,实际上 等同于求解 x = cotx ;
result
构造递推数列 An+1 = (An+cotAn)/2
让我们来验证一下这个数列的有效性。

有界性

对于 An >0 , An+cotAn 导数为 1 + -1／sinx^2 < 0 因此 An+cotAn 是一个递减的,它在 π／2取最小值 π／2 因此 An+1 = (An+cotAn)/2 恒大于 π／4

单调性

An+1 - An = (cotAn - An)／2 显然不单调, [π／4,π／2]两端取一下就可知道。

一个非单调有界数列如何保证收敛到期望值

的确数列不是单调的,但如果An的有界值能够比 π／4 大,落到交点右半边使得数列单调递减,那么不就成了一个单调递减且有下届的递推数列了嘛？我们可以通过极限的知识

1
2
A∞ =(A∞+cotA∞)/2      
A∞ = cotA∞

换句话说我们设定了一个递推数列,当我递推次数足够多时,数列值会收敛于期望值。

别拦我!上C+++试试

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <iostream>
#include <math.h>
using namespace std;
int main() {
    int i = 0 ;
    double x= 0.01 ;
    while(i<100)
    {
        x = (x+cos(x)/sin(x)) /2 ;
        i++;
        cout <<x <<endl ;
    }
    cout << 2*x*cos(x)<<endl ;
}

迭代记录 初值 10000.1 0.01 0.001 都收敛 这是我没有意料到的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
/Users/bubble/CLionProjects/iterator/cmake-build-debug/iterator
50000.8
24999.9
12499.6
6249.33
3125.26
1561.94
781.751
389.972
196.123
98.1767
49.5864
24.1737
11.7361
5.41103
2.28553
0.708868
0.937482
0.835843
0.86986
0.856875
0.861623
0.859858
0.86051
0.860268
0.860358
0.860325
0.860337
0.860332
0.860334
0.860333
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
0.860334
1.12219  这个是 2*x*cos(x) 的值 ／前面都是 x 的迭代值

Process finished with exit code 0

他对于初值的要求似乎没我想的这么高,这是我没有想到的,这其中肯定有说法,有时间来证明.

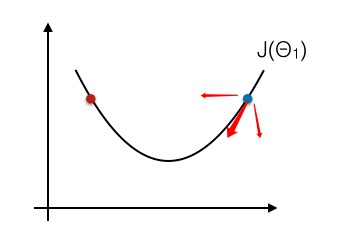
解法二: 梯度下降

和小黑聊起,被告知的,其实在系统辨识中学到过,但我没好好听.感觉亏了.

原理图:这个就相当于你要找一个最拟合的点,你从一个点开始根据导数满满的滑下来,但是找到的永远只能是局部最小值,当局部最小不是全局最小时,这个算法是无效的.

result

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <iostream>
#include <math.h>
using namespace std;
int main() {
    int i = 0 ;
    double x= 0.02 ;
    while(i<1000)
    {
        x = x+0.01*(cos(x)-x*sin(x) ) ;
        i++;
    }
    cout << 2*x*cos(x) <<endl;
}

每次迭代的结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
/Users/bubble/CLionProjects/iterator/cmake-build-debug/iterator
0.039988
0.05994
0.0798323
0.0996413
0.119344
0.138917
0.15834
0.17759
0.196648
0.215495
0.23411
0.252479
0.270583
0.288409
0.305942
0.323171
0.340083
0.356668
0.372919
0.388827
0.404386
0.419591
0.434437
0.448922
0.463044
0.476801
0.490194
0.503223
0.51589
0.528198
0.540148
0.551745
0.562993
0.573897
0.584461
0.594692
0.604595
0.614176
0.623442
0.6324
0.641056
0.649418
0.657492
0.665286
0.672808
0.680064
0.687061
0.693808
0.700311
0.706577
0.712614
0.718429
0.724028
0.729419
0.734608
0.739602
0.744407
0.74903
0.753476
0.757752
0.761864
0.765817
0.769617
0.77327
0.77678
0.780153
0.783394
0.786508
0.789499
0.792372
0.795132
0.797782
0.800327
0.80277
0.805116
0.807368
0.80953
0.811606
0.813598
0.81551
0.817345
0.819105
0.820795
0.822417
0.823972
0.825465
0.826897
0.828272
0.82959
0.830854
0.832067
0.833231
0.834347
0.835418
0.836445
0.837429
0.838374
0.83928
0.840149
0.840982
1.12142       这个是 2*x*cos(x) 的值 ／前面都是 x 的迭代值
              实际上 上述 0.01太小了 使得这个方法迭代的速率很慢
Process finished with exit code 0